fmesher: Triangle Meshes and Other Geometry Tools

CRAN status inlabru-org r-universe status R build status test-coverage Codecov test coverage

Generate planar and spherical triangle meshes, compute finite element calculations for 1- and 2-dimensional flat and curved manifolds with associated basis function spaces, methods for lines and polygons, and transparent handling of coordinate reference systems and coordinate transformation, including sf and sp geometries. The core fmesher library code was originally part of the INLA package, and also distributed in the EUSTACE Horizon 2020 project, and implements parts of “Triangulations and Applications” by Hjelle and Dæhlen (2006). The expanded crs/CRS support started as an add-on feature of inlabru.

Installation

You can install the current CRAN version version of fmesher:

install.packages("fmesher")

Installation using pak

You can install the latest bugfix release of fmesher from GitHub with:

# install.packages("pak")
pak::pkg_install("inlabru-org/fmesher@stable")

You can install the development version of inlabru from GitHub with

pak::pkg_install("inlabru-org/fmesher")

or track the development version builds via inlabru-org.r-universe.dev:

# Enable universe(s) by inlabru-org
pak::repo_add(inlabruorg = "https://inlabru-org.r-universe.dev")
pak::pkg_install("fmesher")

This will pick the r-universe version if it is more recent than the CRAN version.

To install and run fmesher in full debug mode (this is quite an experience!), use

# install.packages("pkgbuild")
source("https://raw.githubusercontent.com/inlabru-org/fmesher/devel/misc/build.R")
fmesher_install(repo = "inlabru-org/fmesher", debug = TRUE)

Installation using remotes

You can install the latest bugfix release of fmesher from GitHub with:

# install.packages("remotes")
remotes::install_github("inlabru-org/fmesher", ref = "stable")

You can install the development version of fmesher from GitHub with

remotes::install_github("inlabru-org/fmesher")

or track the development version builds via inlabru-org.r-universe.dev:

# Enable universe(s) by inlabru-org
options(repos = c(
  inlabruorg = "https://inlabru-org.r-universe.dev",
  getOption("repos")
))
install.packages("fmesher")

Online documentation

https://inlabru-org.github.io/fmesher/

Examples

2D triangular meshes

Refined constrained Delaunay triangulations can be constructed by fm_rcdt_2d() and fm_mesh_2d(). The _inla() versions of these will usually return the same meshes as the old INLA methods, INLA::inla.mesh.create() and INLA::inla.mesh.2d().

suppressPackageStartupMessages(library(fmesher))
suppressPackageStartupMessages(library(ggplot2))

bnd <- fm_extensions(cbind(0, 0), convex = c(1, 1.5))
(mesh <- fm_mesh_2d_inla(
  boundary = bnd,
  max.edge = c(0.2, 0.5)
))
#> fm_mesh_2d object:
#>   Manifold:  R2
#>   V / E / T: 269 / 772 / 504
#>   Euler char.:   1
#>   Constraints:   Boundary: 32 boundary edges (1 group: 1), Interior: 44 interior edges (1 group: 1)
#>   Bounding box: (-1.499887, 1.499887) x (-1.499887, 1.499887)
#>   Basis d.o.f.:  269
ggplot() +
  geom_fm(data = mesh) +
  theme_minimal()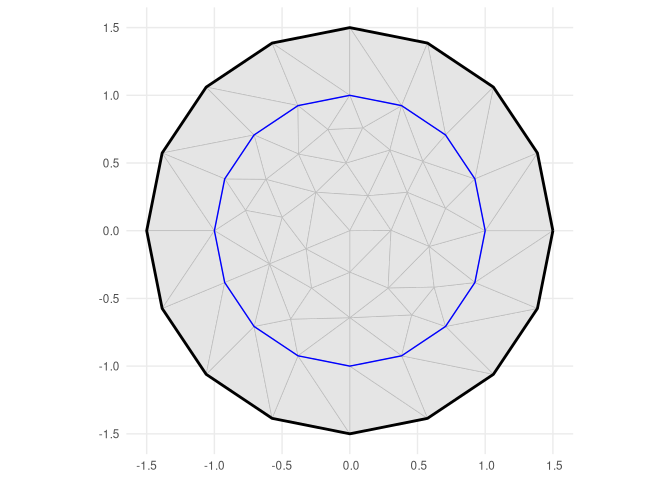

2D triangular mesh

Mostly regular triangulations can be constructed by supplying a regular set of input points. The (experimental, developed by Man Ho Suen) fm_hexagon_lattice() function generates points in a regular hexagonal lattice pattern, contained in a given sf polygon.

hex_points <- fm_hexagon_lattice(bnd = bnd[[1]], edge_len = 0.2)
(mesh_hex <- fm_mesh_2d_inla(
  loc = hex_points,
  boundary = bnd,
  max.edge = c(0.3, 0.5)
))
#> fm_mesh_2d object:
#>   Manifold:  R2
#>   V / E / T: 154 / 427 / 274
#>   Euler char.:   1
#>   Constraints:   Boundary: 32 boundary edges (1 group: 1), Interior: 32 interior edges (1 group: 1)
#>   Bounding box: (-1.499887, 1.499887) x (-1.499887, 1.499887)
#>   Basis d.o.f.:  154
ggplot() +
  geom_fm(data = mesh_hex) +
  theme_minimal()

Quasi-regular 2D triangular mesh

1D B-spline function spaces

(mesh <- fm_mesh_1d(c(1, 2, 3, 4, 6),
  boundary = c("neumann", "free"),
  degree = 2
))
#> fm_mesh_1d object:
#>   Manifold:  R1
#>   #{knots}:  5
#>   Interval:  (1, 6)
#>   Boundary:  (neumann, free)
#>   B-spline degree:   2
#>   Basis d.o.f.:  5
ggplot() +
  geom_fm(data = mesh, xlim = c(0, 7))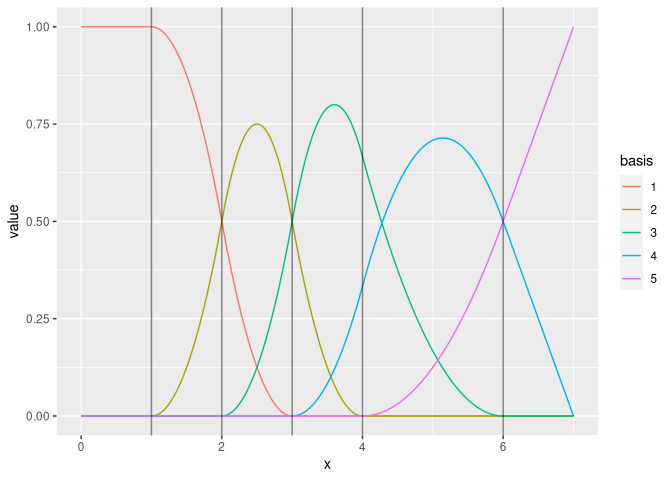

1D B-spline function space

Extended helper methods for CRS handling

The package provides methods fm_crs() and fm_CRS() for extracting CRS information from sf and sp objects and automatically converts to the desired output format. The fm_transform() wrapper similarly handles a variety of objects, as well as special handling for converting between spheres and globes of different radii, e.g. used to map between the Earth and a unit radius sphere uses as a model of the Earth.

# longlat for a spherical version of the Earth
print(fm_proj4string(fm_crs("longlat_globe")))
#> [1] "+proj=longlat +ellps=sphere +no_defs"

# longlat for a sphere of radius 1m
print(fm_proj4string(fm_crs("longlat_norm")))
#> [1] "+proj=longlat +R=1 +no_defs"

# A sphere of radius 1m
print(fm_proj4string(fm_crs("sphere")))
#> [1] "+proj=geocent +R=1 +units=m +no_defs"