Introduzione alla crittografia

ArticleCategory:

System Administration

AuthorImage:

TranslationInfo:[Author and translation history]

original in fr Pierre Loidreau

fr to en Axelle Apvrille

en to it Toni Tiveron

AboutTheAuthor

Pierre lavora come ricercatore tecnico presso l'ENSTA (Ecole Nationale Supérieure de Techniques Avancées). Le sue ricerche riguardano i "crittosistemi" basati sulla teoria dei codici di correzione d'errore. "Gioca" con Linux ogni giorno... ed a tennis abbastanza spesso.

Abstract:

Questo articolo fu pubblicato per la prima volta sul numero speciale sulla sicurezza di Linux Magazine edizione Francese. L'editore ha gentilmente concesso a LinuxFocus di pubblicare ogni articolo di questo speciale. Di conseguenza LinuxFocus vi darà la possibilità di leggerlo non appena questi articolo sono stati tradotti dal francese all'inglese. Ringraziamo tutte le persone che sono coinvolte i questo progetto. Questa breve nota editoriale sarà riprodotta ogni qualvolta troverete un articolo che ha la stessa sorgente.

ArticleIllustration:

ArticleBody:[The article body]

I perchè della crittografia - 2500 anni di storia.

L'origine della crittografia è probabilmente databile all'inizio dell'esistenza umana, nata nel momento in cui le persone impararono a comunicare tra loro. Di conseguenza hanno poi dovuto imparare ad assegnare dei significati ai termini in uso, anche per garantire una certa segretezza nel loro modo di comunicare. Tuttavia il primo uso deliberato di tecniche di crittografia è attribuito ai primi Greci, attorno all'anno 6 A.C.: uno stelo, noto come "scytale", era utilizzato come metodo di codifica e decodifica. Lo scrivente avvolgeva un pezzo di carta attorno allo stelo e, su questo, longitudinalmente vi scriveva il messaggio. A quel punto srotolava la carta e la inviava al ricevente. Per la decodifica del messaggio era necessario conoscere l'esatto diametro dello stelo - che quindi fungeva da chiave segreta - o non sarebbe stato possibile legger correttamente il testo contenuto. In un periodo successivo l'esercito romano utilizzò l'algoritmo di codifica di Cesare (si trattava di un algoritmo basato sullo slittamento di 3 lettere).

Durante i seguenti 19 secoli si è cercato si sviluppare tecniche di cifratura con metodi sperimentali più o meno efficienti. Durante il diciannovesimo secolo, Kerchoffs scrisse i principi della moderna crittografia. Uno dei fondamenti è basato sul fatto che, la sicurezza della crittografia non è basata sul metodo di codifica, ma bensì sulla chiave che si usa per la codifica/decodifica.

Da quel momento in poi, ci si aspettò che i sistemi crittografici rispondessero a questi requisiti. Tuttavia i sistemi di allora mancavano di una base matematica, e di conseguenza anche di strumenti che ne potessero valutare la resistenza ad eventuali attacchi. Si cercava di ottenere un sistema sempre migliore, che fosso sicuro al 100%! Nel 1948 e 1949, si introdusse una base scientifica alla crittografia stessa, grazie a due scritti di Claude Shannon:"Teoria matematica delle comunicazioni" ("A Mathematical Teory of Communications") e l'importante "Teoria delle comunicazioni dei sistemi segreti" ("The Communication Theory of Secrecy Systems"). Questi articoli fecero svanire speranze e pregiudizi. Shannon dimostrò che il sistema crittografico proposto da Verman (noto anche come One Time Pad), pochi anni prima, era l'unico sistema sicuro che potesse mai esistere. Purtroppo questo sistema era irrealizzabile... Questo è anche uno dei motivi per cui, oggigiorno, la valutazione della sicurezza si basa su sistemi computazionali. Si è soliti considerare una chiave sicura allorquando l'unico metodo di attacco possibile sia la ricerca di tutte le possibili chiavi.

AES (Advanced Encryption Standard-Crittografia Standard Avanzata)

Recentemenete, nell'ottobre del 2000, il NIST (National Institute of Standard and Technology - Istituto Nazionale degli Standard e delle Tecnologie), ha annuciato la scelta di adottare un nuovo standard di cifratura tra 15 possibili candidati. Questo nuovo standard nato con lo scopo di sostituire il desueto DES, la cui dimensione delle chiavi di cifratura inizia ad essere troppo piccola. Rijndael - lo strano nome nasce dall'unione dei nomi dei suoi inventori, ovvero Rijmen e Daemen - è stato scelto come il fututo AES.

Questo sistema di crittazione è detto a "bloccchi", in quanto ogni messaggio viene cifrato per mezzo di blocchi a 128bit. Esistono varianti che propongono l'uso di chiavi di cifratura di 128, 192 o 256 bit. Per vostra informazione il sistema DES ricorre a blocchi di 64 bit con chiavi di 56 bit. Il Triple DES (3DES) usualmente utilizza blocchi da 64 bit con chiavi a 112 bit.

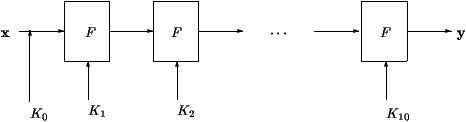
Figura 1: le iterazioni AES
Le modalità operative del sistema AES sono descritte in figura 1. Dapprima il messaggio viene sottoposto all'operazione logica XOR per mezzo della chiave privata K0.Successivamente, per ogni blocco, la funzione F viene iterata, per mezzo di chiavi figlie generate da un processo di espansione attivato dalla chiave master.

Nel caso di AES la funzione F viene iterata 10 volte.

La figura 2 mostra come la funzione F sia iterata per ottenere la crittazione. Un blocco da 128 bit divide i 16 byte avuti come ingresso. La prima permutazione S viene applicata ad ogni byte. Una seconda permutazione P viene applicata ai 16 byte. La chiave figlia a 128 bit, generata dalla funzione di espansione, viene aggiunta per mezzo di un and logico al precedente risultato.
La chiave Ki come intero di n°i si ottiene dalla funzione di espansione utilizzando come sottochiave K(i-1) approssimata a n°i-1 e utlizzando K0 come chiave segreta. La funzione di espansione è descritta in figura 3. I 16 byte della chiave K(i-1) sono processati di 4 in 4.
Gli ultimi 4 byte sono permutati per messo della permutazione S - la stessa permutazione che è stata utilizzata nell'iterazione della funzione F per permutare i bit in ogni byte. Vengono ora aggiunti i primi 4 byte risultanti all'elemento alpha. Questo elemento è un byte predefinito dipendente da un numero intero. Alla fine per ottenere Ki, i risultanti 4 byte sono logicamente sommati ai primi 4 byte di K(i-1). Il risultato viene quindi aggiunto ai 4 byte seguenti.

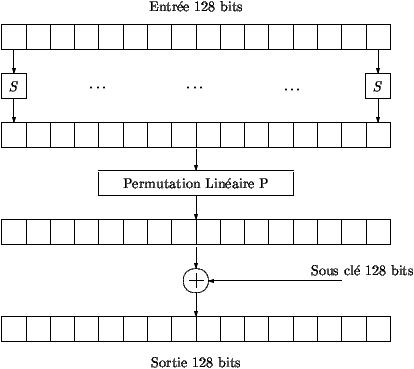
Figura 2: La funzione F
Ora diamo una rapida occhiata a come le sostituzioni vengono attuate e che a cosa serva la costante a ⁱ. Teoricamente - e per semplificare il tutto - un byte dovrebbe esser considerato come un insieme di 256 elementi, che chiameremo elemento finito, su cui si possono fare infinite operazioni (come addizione, moltiplicazione ed inversione) possono essere eseguite. In vero la sostituzione S, precedenetemente menzionata è l'inverso di quel campo. La sostituzione P è definita come una semplice operazione e, di conseguenza, può facilmente essere implementata. L'elemento aⁱ corrisponde con l'elevazione alla potenza di i di un elemento del campo. Questa considerazione permette di rendere l'implementazione di AES molto efficiente.

Dato che AES è basato su semplici operazioni al livello logico, questo porta essenzialmente due grandi vantaggi:

anche le implementazioni al solo livello software sono molto veloci. Per esempio un implementazione scritta in C++ su un Pentium 200 permette un'efficienza di crittogrfia di 70Mbit al secondo;
La resistenza di AES alla criptoanalisi, sia essa lineare o differenziale, non dipende dalla scelta della "scatola" S. Si pensi che queste "scatole", nel caso del protocollo DES, erano sospette di contenere al proprio interno delle backdoor della NSA.

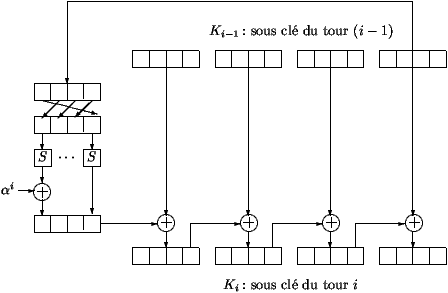
Figura 3: La procedura di espansione

Crittografia a chiave pubblica

Nel 1976 Diffie ed Hellman pubblicarono un articolo "New Directions in Cryptography"("Le nuove strade della crittografia") che fu un vero sconvolgimento per la comunità coinvolta nella crittografia. Questo articolo introdusse il concetto della chiave pubblica nella crittografia. Fino a quel momento l'unico tipo di crittografia nota era basata su algoritmi a chiavi segrete simmetriche, che però non potevano più soddisfare le nuove necessità che si presentavano, anche grazie all'estrema diffusione della rete.

Essenzialmente, l'idea alla base della loro teoria era di introdurre il concetto di una funzione che incoropora un "trabocchetto". Queste funzioni erano semplici da eseguire in un modo, ma dal punto di vista computazionale impossibili da invertire se non si è a conoscenza dello strumento di decodifica , anche se la funzione di codifica è nota a tutti. Si ha quindi che la chiave pubblica agisce come la funzione, ed il "trabocchetto" (che è noto ad un ristretto numero di utenti) è noto come chiave privata. Questo diede luce al mondo di "Alice" e "Bob". Alice e Bob sono due persone che cercando di comunicare tra di loro con le necessità di: integrità dei dati, rendere inutili eventuali accessi al loro flusso di informazioni, sconfiggere eventuali intrusi che vogliano carpire i loro dati, sniffarli o alterarli.

Ovviamente per decifrare il messaggio. il ricevente ha bisogno della funzione inversa, ricorrendo alla chiave privata.

Il più interessante esempio di sistema crittografico, e probabilmente il più semplice, a chiave pubblica fu prensentato dopo due anni, nel 1978. Fu inventato da Rivest, Shamir e Adleman, da cui si ebbe l'acronimo RSA. Esso è basato sulla difficoltà matematica data dalla scomposizione in fattori di un numero intero. La chiave privata è generata da una tripla (p,q,d) con p e q primi, e raffrontabili tra loro (hanno formati simili), e d un intero primo di p-1 e q-1. La chiave pubblica è generata dalla coppia (n,e), con n pari a pq, ed e l'inverso del modulo d (p-1)(q-1). Eccovi un esempio

ed = 1 mod(p-1)(q-1).

Supponiamo che Alice voglia inviare del testo cifrato con la chiave pubblica di Bob (n,e). Dapprima lei trasforma il messaggio in un intero m minore di n. Poi procede con

c = m^e mod n,

ed invia il risultato (c) a Bob. Dal canto suo Bob, la cui chiave pubblica è (p,q,d), esegue la seguente funzione:

c^d mod n = m^ed mod n = m.

Per la codifica RSA, la funzione unidirezionale è la funzione che associa ad un intero x, con x <n, per calcolare x^e mod n.

Dopo il sistema RSA molti altri sistemi a chiave pubblica sono stati inventati. Attualmente la più nota alternativa al sistema RSA è basata su logaritmi discreti.

L'uso moderno della crittografia.

Oggigiorno i sistemi crittografici a chiave pubblica sono molto interessanti sia per la loro semplicità d'uso sia perchè sono in grado di risolvere molti problemi di sicurezza non risolti. Per esser più precisi esso risolve alcuni problemi inerenti l' autentificazione:

Identificazione degli individui: l'utilizzo di connessioni anonime oggigiorno, implica che Alice voglia essere sicura di parlare con Bob e non con qualcuno che si spaccia per lui. Per ottenere questo risultato, lei utilizza un protocollo di identificazione. Molti protocolli di autentificazione esistono oggigiorno e, di norma, si basano sui principi RSA o su logaritmi discreti.
Autentificazione del documento: un'autorità autentifica i documenti per mezzo di una firma digitale. Firmare digitalmente un documento significa aggiungere alcuni bit, che altro non sono che il risultato ottenuto da un funzione che assume come argomenti il documento e l'autorità. Questi bit sono generalmente suddivisi per mezzo di funzioni di divisione come MD5 o SHA. Inoltre, ogni persona che abbia accesso al documento, può essere in grado di verificare che la firma in questione sia stata emessa dall'autorità di identificazione. Per ottenere questa verifica si ricorre a degli schemi di firma. Uno dei più noti schemi è quello di ElGamal - anche questo basato su logaritmi discreti.

Dopotutto un sistema crittografico a chiave pubblica, come pure quello a chiave privata, fornisce sistemi che garantiscono la privatezza delle comunicazioni.

Immaginiamo che Alice voglia comunicare segretamente con Bob. Alice otterrà la chiave pubblica di Bob da un archivio di chiavi pubbliche, e codificherà il proprio messaggio con questa chiave. Quando Bob riceverà il messaggio cifrato, utilizzarà la propria chiave privata per decodificarlo, accedendo così al testo in chiaro scritto da Alice. Entrambe le chiavi hanno compiti diversi, e questo spiega come mai questo tipo di sistemi crittografici sia noto come sistema crittografico assimetrico, diversamente dai sistemi simmetrici che utilizzano la stessa chiave per cifrare e decifrare.

La crittografia a chiave pubblica offre un altro importante beneficio rispetto ai sistemi a chiave simmetrica. Infatti se n utenti comunicano per mezzo di sistemi chiave segreta, ognuno di essi ha bisogno di una diversa chiave per ogni persona del gruppo. Si viene così ad avere la necessità di avere n(n-1) diverse chiavi. Se n è un valore superiore al migliaio, a quel punto si dovrà avere a che fare con un sistema che si destreggia tra milioni di chiavi. Per giunta aggiungere un utente al gruppo si muta in un processo asasi complesso, i quanto si dovranno generare n nuove chiavi per permettere a tutti gli utenti del gruppo di comunicare. In aggiunta a ciò, tutte le nuovi chiavi generate dovranno essere distribuite al gruppo. Al contrario nei sistemi asimmetrici, n chiavi pubbliche dei membri sono memorizzate su si un sistema a pubblico accesso. Aggiungere un utente significa semplicemente aggiungere una nuova chiave a questo sistema.

Ricorrere a chiavi segrete o pubbliche: trovare una via di mezzo

Il paragrafo precedente ci evidenziato come il sistema a chiave pubblica possa risolvere problemi che il sistema a chiave segrete non è in grado di fare. A questo punto qualcuno potrebbe chiedersi l' utilità di un sistema come AES. Vi sono due principali motivi per questa seconda scelta.

Primo: una ragione pratica. Di norma i sistemi a chiave pubblica sono molti lenti. Per esempio il software utilizzato per implementare RAS è un migliaio di volte più lento di quello per AES. RAS, oltrettuto, non fu mai studiato per potere essere implementato a livello hardware. Trasmettere informazioni oggigiorno è talmente cruciale che non possiamo accettare alcun limite agli algoritimi di cifratura.
Secondo: i sistemi di crittografia a chiave pubblica hanno intrinsechi problemi di sicurezza.

Per esempio un sistemi a chiave pubblica richiede una chiave di dimensioni elevate per un corretto livello di sicurezza - se raffrontata a quella segreta. Attualmente si dovrebbe considerare l'importanza della lunghezza della chiave solo se si sta valutando un sistema a chiavi segrete. Infatti questi sistemi si basano sul fatto che solo un brutale attacco possa violarne i codici. Per attacco brutale, in tal caso, si intende l'enumerazione di tutte le possibili chiavi. Se la lunghezza della chiave è di 128 bit, allora si dovranno provare al massimo 2¹²⁸ chiavi.

Per quel che riguarda i sistemi crittografici a chiave pubblica, la dimensione della chiave diviene un parametro interessante solo quando si considera lo stesso sistema. Per esempio, un sistema RSA con chiave a 512 bit è meno sicuro di un sistema AES a 128. L'unico modo per valutare correttamente un sistema a chiave pubblica è quello di verificare la complessità del miglior attacco attuabile. Questo ha molte implicazioni: nessuno sa quando una nuova invenzione possa compromettere la sicurezza di un sistema. Di recente un gruppo di ricercatori ha generato con successo un intero a 512 bit, di conseguenza, per un corretto livello di sicurezza, si dovrebbe ricorrere ad una chiave con numero a 1024 bit.

Di conseguenza, per l'aspetto prettamente inerente la cifratura, gli algoritmi basati su chiavi segrete sono preferibili, ove si possano usare. Zimmermann ha lavorato ad una soluzione ibrida che ha implementato in PGP (PGP utiliza IDEA). Per semplificare, quando Alice e Bob vogliono comunicare con sicurezza ricorreranno ad un algoritmo a chiave segreta:

Alice e Bob stabiliscono una chiave segreta per mezzo di un protocollo di scambio chiavi. I protocolli di scambio chiavi ricorrono alla crittografia a chiave pubblica. Uno dei più famosi protocolli si basa sull'algoritmo di Diffie-Hellman.
A questo punto Alice e Bob comunicano ricorrendo al protocollo IDEA.

Quando hanno finito di comunicare, la chiave utilizzata viene dismessa. Questo genere di sistemi utilizza sia sistemi crittografici a chieve pubblica sia sistemi a chiave segreta. Di solito le persone considerano la parte meno sicura di un tale sistema la procedura inerente il protocollo di scambio di chiavi.

Bibliografia

Storia della crittografia :

S. Singh : Histoire des codes secrets. Jean-Claude Lattès, 1999.
D. Kahn : The Codebreakers: the story of secret writing. MacMillan publishing, 1996.

For AES :

La crittografia in generale :

Un articolo di Anne Canteaut e di Fran Lévy-dit-Véhel : http://www-rocq.inria.fr/canteaut/crypto_moderne.pdf
B. Schneier : Applied Cryptography. John Wiley and Sons, 1996.