笛卡尔树 本文介绍一种不太常用,但是与大家熟知的平衡树与堆密切相关的数据结构——笛卡尔树。
笛卡尔树是一种二叉树,每一个结点由一个键值二元组
(图源自维基百科)
上面这棵笛卡尔树相当于把数组元素值当作键值
其实图中的笛卡尔树是一种特殊的情况,因为二元组的键值
构建 栈构建 我们考虑将元素按照键值
具体不解释,我们直接上图。图中红色框框部分就是我们始终维护的右链:
显然每个数最多进出右链一次(或者说每个点在右链中存在的是一段连续的时间)。这个过程我们可以用栈维护,栈中维护当前笛卡尔树的右链上的结点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次,复杂度
新建一个大小为 n 的空栈。用 top 来标操作前的栈顶,k 来标记当前栈顶。
For i := 1 to n
k := top
While 栈非空 且 栈顶元素 > 当前元素
k--
if 栈非空
栈顶元素.右儿子 := 当前元素
if k < top
当前元素.左儿子 := 栈顶元素
当前元素入栈
top := k
for ( int i = 1 ; i <= n ; i ++ ) { int k = top ; while ( k > 0 && h [ stk [ k ]] > h [ i ]) k -- ; if ( k ) rs [ stk [ k ]] = i ; // rs代表笛卡尔树每个节点的右儿子
if ( k < top ) ls [ i ] = stk [ k + 1 ]; // ls代表笛卡尔树每个节点的左儿子
stk [ ++ k ] = i ; top = k ; }
笛卡尔树与 Treap 谈到笛卡尔树,很容易让人想到一种家喻户晓的结构——Treap。没错,Treap 是笛卡尔树的一种,只不过
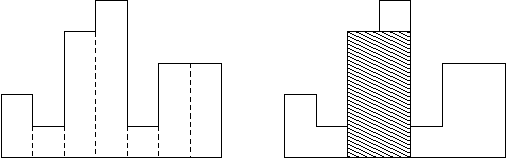
例题 HDU 1506 最大子矩形
题目大意:
阴影部分就是图中的最大子矩阵。
这道题你可 DP,可单调栈,但你万万没想到的是它也可以笛卡尔树!具体地,我们把下标作为键值
这样我们枚举每个结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56 #include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std ; typedef long long ll ; const int N = 100000 + 10 , INF = 0x3f3f3f3f ; struct node { int idx , val , par , ch [ 2 ]; friend bool operator < ( node a , node b ) { return a . idx < b . idx ; } void init ( int _idx , int _val , int _par ) { idx = _idx , val = _val , par = _par , ch [ 0 ] = ch [ 1 ] = 0 ; } } tree [ N ]; int root , top , stk [ N ]; ll ans ; int cartesian_build ( int n ) { // 建树,满足小根堆性质
for ( int i = 1 ; i <= n ; i ++ ) { int k = i - 1 ; while ( tree [ k ]. val > tree [ i ]. val ) k = tree [ k ]. par ; tree [ i ]. ch [ 0 ] = tree [ k ]. ch [ 1 ]; tree [ k ]. ch [ 1 ] = i ; tree [ i ]. par = k ; tree [ tree [ i ]. ch [ 0 ]]. par = i ; } return tree [ 0 ]. ch [ 1 ]; } int dfs ( int x ) { // 一次dfs更新答案就可以了
if ( ! x ) return 0 ; int sz = dfs ( tree [ x ]. ch [ 0 ]); sz += dfs ( tree [ x ]. ch [ 1 ]); ans = max ( ans , ( ll )( sz + 1 ) * tree [ x ]. val ); return sz + 1 ; } int main () { int n , hi ; while ( scanf ( "%d" , & n ), n ) { tree [ 0 ]. init ( 0 , 0 , 0 ); for ( int i = 1 ; i <= n ; i ++ ) { scanf ( "%d" , & hi ); tree [ i ]. init ( i , hi , 0 ); } root = cartesian_build ( n ); ans = 0 ; dfs ( root ); printf ( "%lld \n " , ans ); } return 0 ; }
参考资料 维基百科 - 笛卡尔树
build 本页面最近更新:2021/8/12 19:24:54 ,更新历史 edit 发现错误?想一起完善? 在 GitHub 上编辑此页! people 本页面贡献者:Enter-tainer , ouuan , sshwy , StudyingFather , AngelKitty , GavinZhengOI , Ir1d , kenlig , ksyx , ouuan , zhouyuyang2002 copyright 本页面的全部内容在 CC BY-SA 4.0 和 SATA